电脑在进行求和运算时,有时会出现错误结果的情况,这对于需要高精度计算的领域来说是不可接受的。本文将探讨电脑求和错误的主要原因,并提供解决该问题的有效方法。
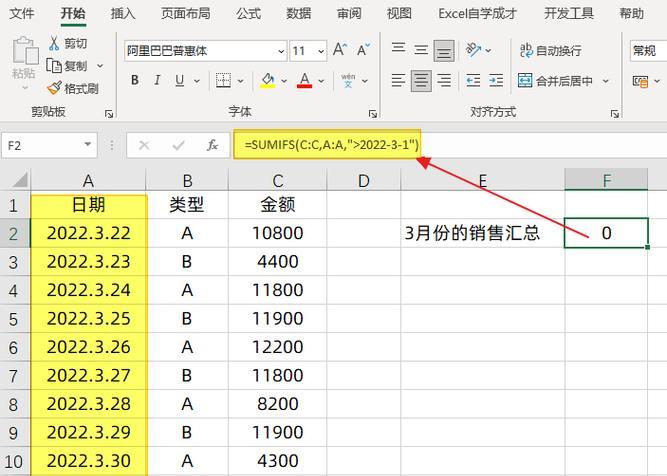
1.精度问题:电脑求和错误往往源于计算机内部对于小数的存储方式。由于计算机内部采用二进制存储,无法精确表示一些十进制小数,从而导致求和结果产生误差。
2.舍入误差:在进行浮点数运算时,计算机会对结果进行舍入,从而引发求和错误。舍入误差是指计算机在进行浮点数运算时,将无限循环小数或无限不循环小数截断为有限位数,导致最终结果与真实值存在差异。
3.运算顺序错误:求和过程中的运算顺序可能会影响最终结果的精度。根据运算法则,先进行较大的数相加,再进行相加的结果与较小的数相加,可以避免由于数值范围过大或过小而引发的求和错误。
4.数值溢出:当进行大规模求和时,如果计算结果超过计算机内部所能表示的范围,就会导致数值溢出错误。数值溢出是指计算结果超出计算机内部所能表示的最大值或最小值,导致结果不准确或直接无法表示。
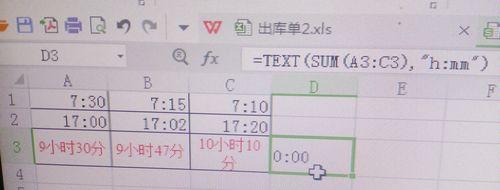
5.误差传递:当多个数相加时,每个数本身的误差会被累积传递,导致最终结果的误差比单独相加的误差更大。由于计算机内部存储浮点数的方式以及运算精度限制,多次求和会将每次求和的误差累积起来,最终导致结果的误差越来越大。
6.浮点数标准:浮点数运算中采用的IEEE754标准定义了浮点数的存储结构和运算规则,但该标准也存在一些问题。IEEE754标准虽然规定了浮点数的存储结构和运算规则,但其中的舍入规则和舍入方式并不一定适用于所有求和场景,从而可能导致求和错误。
7.浮点数精度控制:为了减小求和错误的发生概率,可以通过控制浮点数的精度来提高计算结果的准确性。通过控制浮点数的有效位数,可以减少舍入误差的发生,并提高求和结果的精度。
8.运算顺序优化:在进行多个数相加时,合理调整运算顺序可以降低求和错误的风险。通过优化运算顺序,将较大的数相加放在前面,较小的数相加放在后面,可以减小误差传递和数值溢出的可能性。
9.精确求和算法:针对需要高精度求和的场景,可以采用特殊的算法来降低求和错误。例如,可以使用Kahan算法或其他高精度求和算法,通过补偿误差项来提高结果的准确性。
10.高性能计算:对于大规模求和的需求,可以借助并行计算或分布式计算等高性能计算方法来提高结果的精度和计算速度。通过利用多个计算节点的并行计算能力,可以在保证求和结果准确性的同时,提高计算效率。
11.软件工具辅助:现有的数值计算软件中通常提供了精确求和、高精度计算等功能,可以借助这些工具来规避求和错误。通过使用现有的数值计算软件,例如MATLAB或Python的NumPy库,可以方便地进行精确求和和高精度计算,减少求和错误的发生。
12.数据预处理:对于需要进行大规模求和的数据集,可以在进行求和前进行数据预处理,以减小求和错误的影响。例如,对数据进行归一化处理、去除异常值或进行合理的数据压缩,可以提高求和结果的准确性。
13.误差分析与调试:当求和结果出现错误时,应进行误差分析和调试来定位问题并找到解决方法。通过对每次求和的输入数据、运算过程以及输出结果进行仔细分析,可以找到导致求和错误的具体原因,并采取相应措施进行修正。
14.精度与效率的权衡:在实际求和过程中,需要根据具体需求对精度和计算效率进行权衡。较高的精度通常伴随着较大的计算代价,因此需要根据实际情况选择合适的精度和计算策略,以达到满足需求的最佳平衡点。
15.电脑求和错误是由于精度问题、舍入误差、运算顺序错误、数值溢出、误差传递等原因引起的,可以通过控制精度、优化运算顺序、采用精确求和算法、借助高性能计算、使用软件工具辅助等方式来解决。在实际应用中,需要根据具体需求和计算条件进行相应的调整,以达到精确求和和高效计算的目标。
标签: 求和错误

